Bir Doğal Sayının Karesi ve Küpünün Hesaplanması
5. Sınıf matematik dersinde gösterilmeye başlanan üslü ifadeler öğrenciler tarafından oldukça sevilmekte ve yapılması kolay olan konular arasında gösterilmektedir. Bu konumuzda bir doğal sayının karesini ( 2. kuvvetini) ve küpünü hesaplamayı öğreteceğiz.
Tekrarlı çarpımlar olarakta adlandırılan üslü ifadeler bir doğal sayının ard arda kendisiyle çarpımı olarak bilinmelidir. Taban ve üs olarak iki bölümden oluşan bu ifadeler üs kadar tabanın sırayla çarpılması ile hesaplanabilmektedir. Gelin öncelikle üslü ifade nedir? bu konuya değinelim.
ab şeklinde yazılabilen matematiksel ifadelere üstlü ifade denir. Burada a harfi tabanı, b harfi ise üssü(kuvvet) belirtmektedir. Üste bulunan sayı kaç adet ise tabandaki sayı o kadar yan yana yazıp çarpılır.

Hesaplama işlemine geçmeden önce öncelikle bu sayıların nasıl okunduğuna değinelim. Şimdiye kadar sayının üstünde başka bir sayı görmemiş olduğunuzdan bu sayıların yanlış yazıldığı hissine kapılmış olabilirsiniz. Fakat yukarıdaki kısa özetimizle aklınızda ufakta olsa bir şeyler canlanmıştır. Sırada bu ifadelerin nasıl okunduğu var…
Üslü İfadelerin Okunuşları
- Tekrarlı çarpımları okurken önce tabanı daha sonra da üssü kelimesi ardından yukarıda bulunan sayıyı söyleriz.
- Önce taban daha sonra “üzeri” kelimesi ardından üste bulunan sayı okunur.
- Alternatif olarakta tabanda bulunan sayının üste bulunan sayıncı kuvveti şeklinde okunabilir.
| İfadeler | Okunuşları |
| 34 | 3 üssü 4 3 üzeri 4 3’ün 4. kuvveti |
| 25 | 2 üssü 5 2 üzeri 5 2’nin 5. kuvveti |
| 26 | 2 üssü 6 2 üzeri 6 2’nin 6. kuvveti |
Bu okunuşlara istisna oluşturan ve öğretmenlerimizin ağzından sürekli çıkan, bizimde sürekli kullanacağımız daha farklı okunuşlar bulunmaktadır.
- Bir sayının üzerinde “2” bulunuyorsa taban söyledikten sonra “karesi” kelimesi okunur.
- Bir sayının üzerinde “3” bulunuyorsa taban söyledikten sonra “küpü” kelimesi söylenir.
| İfade | Özel Okunuşu |
| 32 | 3 ‘ün karesi |
| 52 | 5 ‘in karesi |
| 43 | 4 ‘ün küpü |
| 53 | 5 ‘in karesi |
| 23 | 2 ‘nin küpü |
| 42 | 4 ‘ün karesi |
| 122 | 12 ‘nin karesi |
Doğal Sayıların Kareleri Hesaplanması
Sayıların kareleri hesaplanmadan önce kare kelimesinin 2. kuvveti belirttiğini yukarıda anlatmıştık. Çok basit bir deyişle karesi hesaplanırken tabandaki sayı 2 defa yazılır ve çarpılır.
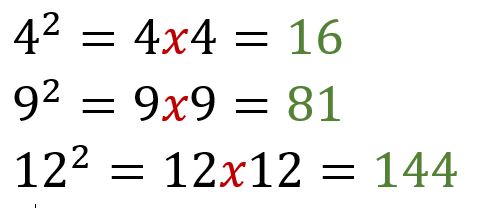
Şimdi de çok kullanılan 2. kuvveti ile çok karşılaştığımız sayıların hesabını yapalım.
0’ın karesi kaçtır?
02= 0 x 0 olduğundan sıfırın karesi sıfıra eşittir.
1’in karesi kaçtır?
12 = 1 x 1 olduğunda cevap 1 olacaktır.
2 ‘nin karesi
22= 2 x 2 = 4 olduğundan 4’e eşittir.
3 ‘ün karesi
32= 3 x 3 = 9 olduğundan 9’a eşittir.
4 ‘ün karesi
42 = 4 x 4 = 16 olduğundan 16’ya eşittir.
5 ‘in karesi
52= 5 x 5 = 25 olduğundan 25’e eşittir.
6 ‘nın karesi kaçtır?
62= 6 x 6 = 36 olduğundan 36 ‘dır.
Doğal Sayıların Küpleri
Bir sayının küpünden bahsettiğimiz zaman o sayının üçüncü kuvveti olduğunu işlemiştik. Bir sayının küpünü hesaplamak için tabanda bulunan sayıyı 3 defa yazıp çarpmalıyız. Örnekler ile gösterecek olursak;

Yukarıdaki alıştırmalarda da görüldüğü gibi sayılar ilk çarpımın sonucuyla tekrar çarpılarak sonuç bulunuyor. Karesini hesaplamaya göre biraz daha kafa karıştırıyor gibi olsa da aşağıdaki örnekleri incelediğinizde kafanızda her şeyin oturacağının garantisini veriyorum.
2 ‘nin küpü kaçtır?
2 üssü 3 ifadesini öncelikle matematiksel olarak yazalım ve sonra hesaplayalım.
23 = 2 x 2 x 2 = 8 . Kısacası işlemi anlatacak olursak ilk 2 tane 2 çarpıldığında sonucu 4 olarak bulacağız. Sonra o 4 sayısı ile son kalan yani 3. 2 sayısını çarptığımızda 4 kere 2 = 8 olacaktır.
3 ‘ün küpü
3 üzeri 3 olarakta okunabilen üslü ifade şu şekilde hesaplanır. 33 = 3 x 3 x 3 = 27 . İlk olarak iki tane 3’ü birbiri ile çarparsak cevabı 9 bulur, onu da son kalan 3 ile çarparsak cevabımızı 27 olarak hesaplayacağız.
4 ‘ün küpü
43 = 4 x 4 x 4 olarak yazılıp işlemler sıra ile çarpıldığında 64 cevabına ulaşırız.
5 ‘in küpü
53 = 5 x 5 x 5 = 125
6 ‘nın küpü
63 = 6 x 6 x 6 ilk iki altının çarpımı 36 yapıp, sonraki 6 ile çarptığımızda sonucu 216 olarak bulmaktayız.
Üslü ifadelerin hesaplamaları sadece kare ve küpü ile sınırlı değildir. Fakat şimdilik ( 5. sınıfta) bu kadarını bilmeniz yeterli olup farklı kuvvetlerin hesaplamalarını 6. ve 7. sınıf düzeyinde öğreneceksiniz. Umarım konuyu öğrenebilmişsinizdir. Bu konu ile ilgili aklına takılan her soruyu yorum bölümünden bize sorabilir, cevabımızı bekleyebilirsin.



